Making mead is easy. You mix together honey and water, rehydrate and pitch your yeast, aerate, and add some yeast nutrient at scheduled times during the first few days of fermentation. After a few weeks, you rack to a secondary for aging. Within a year (maybe less), you have a drinkable mead (although age will continue to improve the mead for many months and years). But how much honey exactly do you need to make mead? In this post, we’ll answer just that, and point you to a nifty calculator to anticipate the amount of honey you’ll need to make mead.

The Simple Answer

Each pound of honey added to a gallon of must (the pre-fermentation honey and water mixture) adds about 5% of potential alcohol when fermented completely. Each pound of honey also adds about 35 gravity points, bringing the must original gravity from that of water, 1.000, to 1.035 (specific gravity is a measure of the density of a fluid compared to water). This means each alcohol percentage point is approximately 7 gravity points when planning your batches. Using these numbers, we can calculate an expected alcohol content and final gravity (to determine sweetness level).

To explore the possibilities, we present two examples below from the same starting parameters, but fermenting with a different yeast. For a list of appropriate mead yeasts, check out our Mead Yeast Primer.

Example 1

A typical mead batch consists of 15 pounds of honey for a 5 gallon mead batch. In this example, you have 3 pounds of honey per gallon of must, so your potential alcohol by volume is about 15%. Similarly, you’ll expect that you will have an original gravity of about 1.105 (3 * 35 = 105 gravity points, for an OG of 1.105).

In this example, we will use Lalvin 71b, a 14% alcohol tolerance yeast, to ferment the must. Because the alcohol tolerance is less than the potential alcohol of the must, we expect to have some residual sweetness leftover:

15% must potential ABV – 14% yeast ABV tolerance = 1% residual sweetness

This 1% residual sweetness means you have a dry to semi-sweet mead, with a final gravity around 1.007.

Example 1 Batch Specifics:
15 pounds honey
5 gallon batch
Lalvin 71b Yeast with 14% Alcohol Tolerance
Starting Gravity: 1.105
Final Gravity: ~1.007
Sweetness Level: Dry to Semi-Sweet

Example 2

So, say you wanted to make the same must (3 pounds of honey per gallon), but swapped out the yeast. How does this impact your final mead? We’ll use a higher alcohol tolerance yeast to show you, fermenting with Lalvin K1-V1116 with an alcohol tolerance of 18%.

Again, we have a potential alcohol of 15% from the honey, but here our yeast tolerance is higher than the potential, so the yeast will ferment the batch completely dry. There will be no residual sweetness after fermentation, and the final gravity should end up around 1.000, although it will likely be less (read the Advanced Answer section below for more information).

Example 2 Batch Specifics:
15 pounds honey
5 gallon batch
KI-V116 Yeast with 18% Alcohol Tolerance
Starting Gravity: 1.105
Final Gravity: ~1.000
Sweetness Level: Dry

The Advanced Answer

The simple approximation of honey’s contribution to mead above works in many cases, and will provide most meadmakers with a solid foundation for making mead. However, the assumptions made in the calculation do not hold true across the entire range of potential alcohols and honey contributions. Let’s explore some of these limitations.

The Sugar Content of Honey

First, mead calculators assume you have approximately 79.6% sugar content in your honey. This is a good basis, and many honey packers will modify the water content to produce honey around this sugar level. However, minimally processed honey does not have 79.6% honey, due to the different floral sources and environmental humidity levels (honey is the byproduct of nectar, and not all nectars are created equal). In The Compleat Meadmaker, Ken Schramm provides a table of varietal honey compositions, showing that in 44 honey varieties the sugar content varied between 74% and 82%, with 79.6% equaling the average sugar content. (The source material for this table can be found in Composition of American Honeys, Technical Bulletin 1261, but Ken’s summary table is much better for day to day use.)

A range of 74% to 82% may not sound like much, so let’s explore the impact this will have on approximating alcohol content.

Using Bates et al (Bates), we can determine the specific gravity (SG) of a 74% sugar solution, 79.6% sugar solution, and 82% sugar solution, to model the SG of honey (note, it has been shown that the other dissolved solids in solution have minimal impact on SG, see here). We’ll next take the SG and determine the volume of 1 pound of honey so that we can understand the amount of gravity points associated with adding each pound of honey to a 1 gallon must. The total batch volume will be 1 gallon, regardless of the volume of 1 pound of honey. To see the difference between these values, check out the table below. For an approximation of SG as a function of water content in the honey, see here.

Honey Sugar Content	SG of Honey	SG of 1 gal must with 1 lb honey	SG of 1 gal must with 3 lb honey
74%	1.37541	1.033	1.098
79.6%	1.41204	1.035	1.105
82%	1.42138	1.036	1.107

So at first glance, this doesn’t look like much impact. For a single pound honey per gallon must, the difference is only 3 gravity points across the entire range. Multiply that for our example batches in the section above, however, and that range becomes 9 gravity points. This means that depending on your honey source, you could be as much as 1.29% off in your alcohol by volume calculations.

To avoid this problem and ensure consistency batch to batch, measure and plan your batches using SG or Brix from a trusty hydrometer or refractometer. Using an SG or Brix measurement circumvents the issue with different sugar contents, and ensures the same amount of sugar is always present in the must regardless of the sugar content of the honey.

Sugar types in Honey

Another thing to remember about honey is that it is made up of many different sugar types. On average, you have the following breakdown of sugars, however individual honeys will differ:

Sugar Type	% by weight
Levulose	38.19
Dextrose	31.28
Sucrose	1.31
Maltose	7.31
Higher Sugars	1.5

This isn’t terribly important in many cases, however some yeasts will prefer to “fatten” themselves up on one type of sugar over another, to the extent that they may not process all of the sugars available to them. Specifically, maltose is not as readily fermented by wine yeasts, even though it is a favorite for beer yeasts. So while you have available sugar to the wine yeast in the form of maltose, it may not ferment depending on the yeast strain. This would leave you with some residual sugar unless another yeast type were introduced.

Converting Sugar Content to Alcohol

In our How to Determine ABV post, we examined the different means to calculate alcohol by volume. Each method includes certain assumptions about your batch of mead (and wine or beer), exposing the flaws that come with fitting linear models to exponential curves. Specific gravity does not scale linearly with sugar content as proposed above (as you increase the amount of sugar, you don’t continue to get 35 gravity points for each pound addition). Similarly, depending on the efficiency of the fermentation, your yeast may create more or less alcohol than expected. The Cliff’s Notes version of ABV calculation limitations is provided below.

Specific Gravity Does Not Scale Linearly with Sugar Content

In a purely mathematical form, the specific gravity of a solution is a function of the solution’s sugar content, i.e. SG = f(Sugar Content). This holds true for fermentable solutions, based on the assumption that SG is only biased by the content of sugar in solution, and that any other soluble solids do not impact the SG.

Brix, a measure of sugar content in a solution, can then be directly correlated to SG. The Bates study referenced above calculated the SG for sugar content solutions from 0 to 94.5% sugar by weight. The chart below displays the subset of the Bates table as it is applicable to a meadmaker, covering the range of 0 to 38.9 Brix, or roughly 0 to 22.5% ABV.

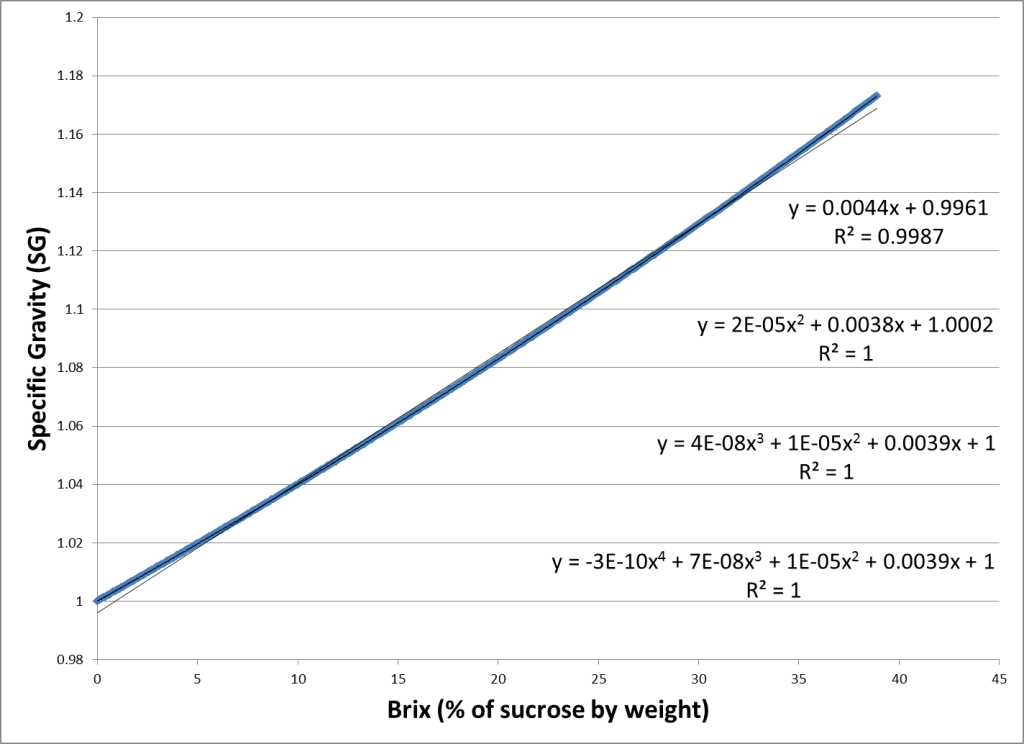
In the chart, we have included the linear, second order, third order, and fourth order polynomial approximations of SG as a function of Brix. It is immediately apparent the linear approximation is not valid for the entire range. Further analysis of the data shows that the third order polynomial is the best estimation of these four models, thus the calculation for SG from Brix becomes the following:

SG = 4.3236*E-8 * (Brix) ^3 + 1.3447E-5 * (Brix) ^2 + 3.8612E-3 * (Brix) + 1

Because the third order approximation better matches the actual SG from the sugar content, we should use this formula to approximate the changes in SG as a function of honey additions to the must. In other words, our 35 gravity points for each pound of honey added to the must is a decent approximation, but a third order function would be a better method to estimate the increase in gravity points for each pound honey.

Efficiency of The sugar to alcohol conversion

The conversion of sugar to alcohol follows the following form:

C₆H₁₂O₆ → 2 C₂H₅OH + 2 CO₂

In this equation, sugar (the left hand side of the equation) is converted into 2 ethanol and 2 carbon dioxide molecules. In a perfect world, this chemical equation takes off without a hitch, and every bit of sugar available is converted into only alcohol and carbon dioxide. However, in actuality, not all of the sugar is converted to alcohol in the final mead. Some is lost due to the yeast population expanding and the yeast cells repairing themselves; some is lost as other chemical byproducts are created; and some is lost to alcohol evaporation to the atmosphere. Studies have shown about a 90% efficiency in converting sugar to alcohol (10% of the sugar is lost to these activities). So of all the sugar available, only 90% is actually converted to alcohol.

Our initial assumptions in the simplified answer already took this estimation into account, but nonetheless this should be considered when calculating the amount of alcohol created from a given quantity of honey.

Introducing the MeadMakr BatchBuildr

If you got lost in the math or chemistry presented above, MeadMakr has you covered. To help with building your mead recipes, we have created the BatchBuildr that takes your desired alcohol content, final gravity (an estimation of sweetness), and the batch volume to estimate the amount of honey you need to make your batch.

For those wanting to know how it works, we use 79.6% sugar content for honey; calculate the original specific gravity (OG) of the must based on your batch volume, desired alcohol content, and final gravity; and convert the OG back to pounds of honey required to create that amount. For repeatability in your batches, use the honey content as an estimation of what is required. Due to variations in honey sugar content, it is strongly advised you build your batches from the OG.

To help with understanding how the BatchBuildr works, and to answer the question of how much honey you need to make a batch, a few examples are provided below.

Example 3

Let’s assume here that we just want to know how much honey we need to make a dry batch of mead, and we want to know how much is needed to make a 5% ABV mead, a 10% ABV mead, and a 15% ABV mead. Recall from our initial simplified answer that we expect to need 1 pound of honey for the 5% mead, 2 pounds for the 10% ABV mead, and 3 pounds for the 15% ABV mead. Let’s check what the calculator says.

To make a dry 5% ABV mead, the BatchBuildr predicts you will need 0.98 lbs honey, and recommends a 1.034 SG to start.

For the 10% ABV dry mead batch, you’ll actually need 2.02 pounds of honey and should have an SG of 1.071.

For the 15% dry mead, you’ll need 3.13 pounds of honey and an original gravity of 1.110.

These are extremely close to the initial estimates of 1 pound of honey for 5% ABV and 35 gravity points provided in the simple solution above. However, when you take into account the changes to SG as a function of sugar content, you start to see variations across the entire fermentable range. The BatchBuildr uses these changes in its approximations, and will ensure you have the right amount of honey for the mead you want to make.

 

I hope you enjoyed this extended exploration into the amount of honey you need to make your mead. Let us know what you think via twitter or in the comments below!